상세 컨텐츠
본문
작성 : 13기 최해윤
Part Ⅰ. Tabular Solution Methods
강화학습의 simplest forms에 대하여 배우는 챕터다. action-value function이 array나 table 형태로 나타나기에 충분할 정도로 그 state와 action space가 작은 형태다. 이러한 경우, optimal value function과 optimal policy를 찾을 가능성이 높다. 이는 오직 approximate solutions만 찾아내는 much larger problems과 대비된다.
강화학습이 다른 학습들과 구분되는 가장 중요한 특징은 correct actions에 대한 정보를 제공하여 instruct 하는 것이 아니라 actions을 평가한다는 것이다. 이것이 곧 active exploration의 필요성을 잘 보여준다. 당장의 reward를 위해 action을 exploit하는 것도 중요하지만 정답이 없는 상황에서 environment와의 communication, 즉 exploration은 장기간에 걸친 reward의 누적량 극대화라는 측면에서 당장의 reward보다 더 중요할 수 있다.
Multi-arm Bandits
Part Ⅰ 첫 번째 챕터로 single state를 갖는 강화학습 문제인 bandit problems에 대해 공부한다.

- state에 대한 정보는 없다. 위 예에서는 각 기계의 수익률에 대한 정보가 없다고 이해하면 쉽다.
- 다른 option을 explore (nongreedy action) 또는 이미 경험한 option을 exploit (greedy action)
- 선택한 행동에 따라 Reward를 받는 일련의 과정을 통해 취득 보상의 기댓값을 높이는 것이 목표다.
Action-Value Methods
Action Value란 특정 시점에서 어떠한 Action을 취했을 때의 Reward에 대한 기댓값이다.
시행착오를 통해 True Reward Distribution을 추측하고 싶다면 어떻게 해야 할까?
Sample-Average Method 라는 다소 직관적인 방법을 도입할 수 있다.
다음을 예로 들어 이해해보자.
약물 임상 실험에서 12회 투약을 통해 3가지 약물 R, G, B의 약효에 대해 조사한다.

다음으로 Epsilon-greedy Algorithm 이 있다.
sample-average method에서는 explore와 exploit을 randomly 결정하였다.
Epsilon-greedy Algorithm에서 epsilon은 적은 확률을 의미하며, 해당 확률로 explore를,
나머지 확률로는 exploit을 진행한다.
앞에서는 이전 reward에 대한 기록들이 모두 존재할 때 계산할 수 있는 방법들로 그 memory와 computation 관점에서 매우 비효율적이다.
Action-value 추정치를 보다 효율적으로 계산하는 법은 없을까? 라는 궁금증에서
Incremental Update Rule 이 등장한다.
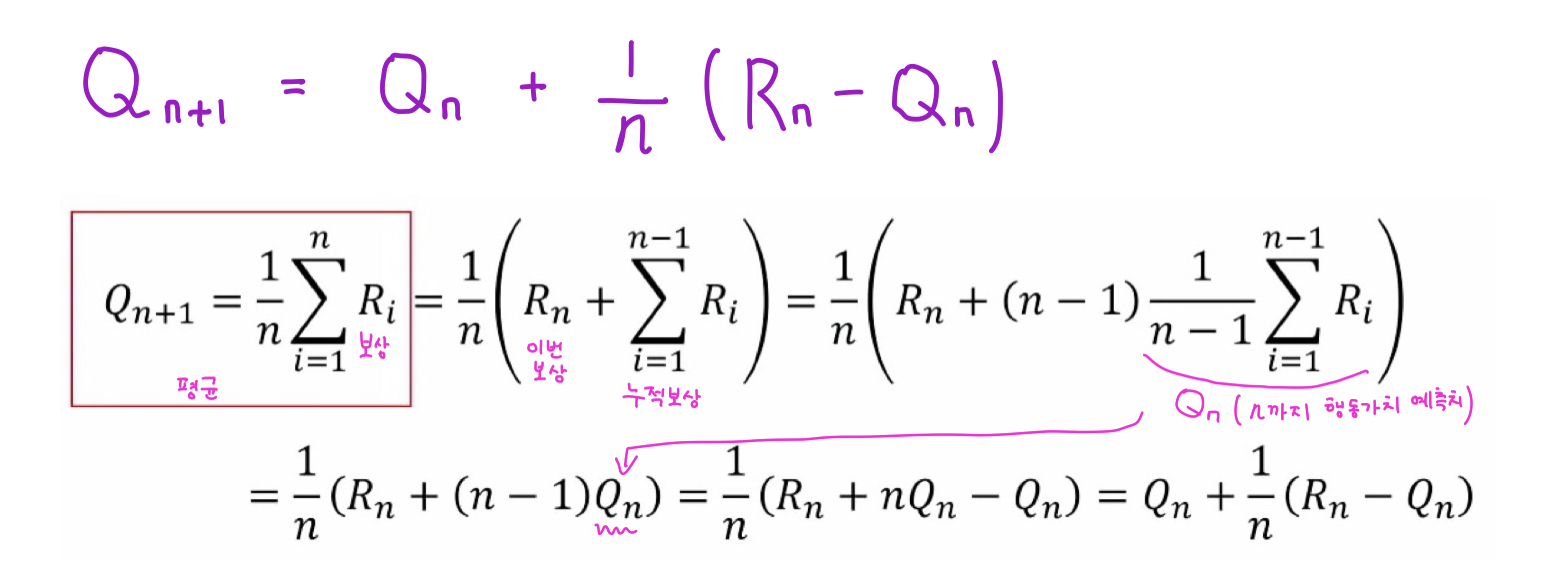
위 수식과 같이 계산하면 Updated = Old + Weight x (New - Old) 로 계산이 가능하다.
이는 기존 정보에 새로운 정보가 들어올 때 Update를 어떻게 하면 좋을지에 대한 아이디어를 제공하며,
강화학습에도 적용이 가능하다.
위 식에서 Weight가 1/n 이라는 것은 해당 Problem이 Stationary Bandit Problem임을 의미한다.
즉, 시간에 따라 reward의 확률이 달라지는 Nonstationary Problem 이라면 어떻게 달라질까?
Weight 자리에 위치했던 1/n이 a로 바뀌고 식은 다음과 같다.

a 값을 조정함으로써 최근에 받은 reward의 가중치를 이전 reward에 비해 키우거나 줄일 수 있다.
Optimistic Initial Values
지금까지 모든 수식들에서 초기값인 Initial Action Value에 영향을 많이 받음을 확인할 수 있다.
이는 Bias로 작용하게 되는데 그 초기값을 0이 아닌 5로 잡으면 실험 결과가 확연히 달라진다.

초기값을 5로 잡으면 앞으로 어떤 Action이 선택되어도 updated reward는 5보다 작을 것이기에
Exploit이 아닌 Explore를 진행할 것이다. 결과를 봐도 explore를 많이 하여 그 성능이 처음에는 낮지만 결과적으로 더 좋은 성능을 보이게 된다.

'심화 스터디 > 강화학습 스터디' 카테고리의 다른 글
| 1. 강화학습이란 ? (0) | 2021.09.16 |
|---|---|
| 0. 강화학습 스터디 개요 (0) | 2021.09.09 |
| 강화학습 스터디 소개 (0) | 2021.08.27 |



댓글 영역